队列是一种特殊的线性表，特殊之处在于它只允许在表的前端进行删除操作，而在表的后端进行插入操作(先入先出原则)，和栈一样，队列是一种操作受限制的线性表。进行插入操作的端称为队尾，进行删除操作的端称为队头。

队列的使用场景

银行排队案例：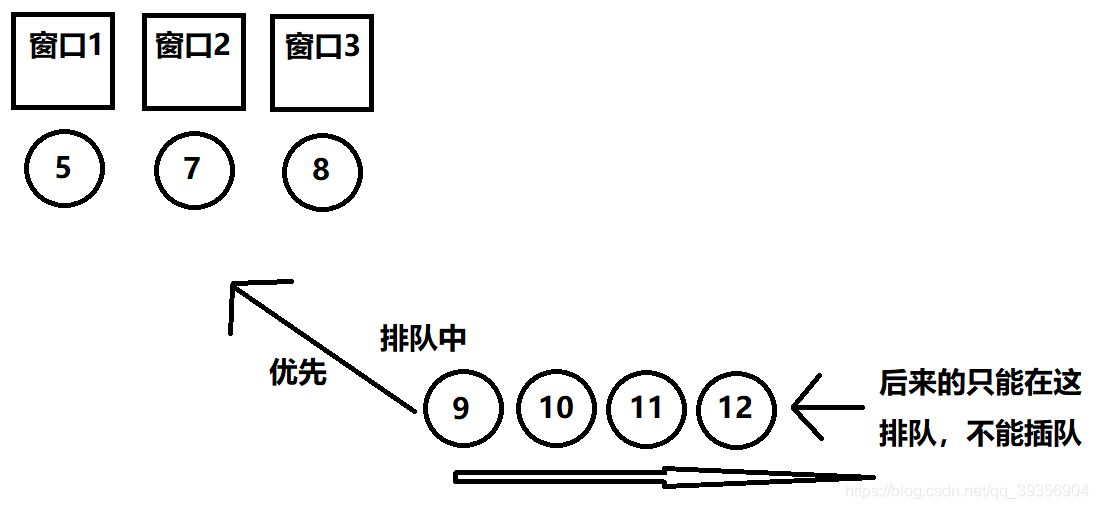
在这里插入图片描述  在银行排队办理业务的时候，如果窗口有人正在办理业务，后面等待的人会按照先后顺序排成一个队列，这个队列的人，先到的先从等待队列中出去办理业务，而后到的人要从这个队列的末尾排队，等待先到的人从这个等待队列出去办理业务之后，后到的人才能从等待队列出去。

用数组模拟队列思路分析

  队列本身是有序列表，若使用数组的结构来存储队列的数据，则队列数组的声明如下图所示，其中maxSize是该队列的最大容量。
  因为队列的输出、输入是分别从前后端来处理，因此需要两个变量front及rear分别记录队列前后端的下标，front会随着数据输出而改变，而rear则是随着数据输入而改变，如图所示：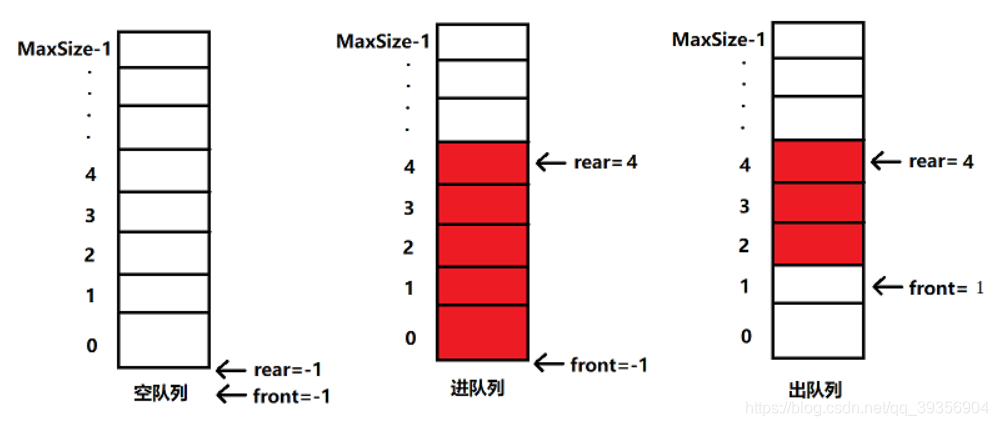
在这里插入图片描述
当我们将数据存入队列时称为“addQueue”，addQueue的处理需要有两个步骤：
(1)将尾指针往后移：rear+1，当front==rear 时，为空队列。
(2)若尾指针rear小于队列的最大下标maxSize-1，则将数据存入rear所指的数组元素中，否则无法存入数据。rear==maxSize-1 时，为队列满。

数组模拟队列的代码实现

模拟一个队列实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
//使用数组模拟队列（编写一个ArrayQueue类）
class ArrayQueue{
	private int maxSize;//表示数组的最大容量
	private int front;//队列头
	private int rear;//队列尾
	private int[] arr;//该数组用于存放队列，模拟的队列
	//创建队列构造器
	public ArrayQueue(int arrMaxSize){
		maxSize = arrMaxSize;
		arr = new int[maxSize];
		front = -1;//指向队列头部，分析出front是指向队列头的前一个位置
		rear = -1;//指向队列尾部，指向队列尾的数据(就是队列最后一个数据)
	}
	//判断队列是否满
	public boolean isFull(){
		return rear == maxSize - 1;
	}
	//判断队列是否为空
	public boolean isEmpty(){
		return rear == front;
	}
	//添加数据到队列
	public void addQueue(int n){
		//判断队列是否满
		if(isFull()){
			throw new RuntimeException("队列满，不能加入数据！");
		}
		rear++;//让rear后移
		arr[rear] = n;
	}
	//数据出队列
	public int getQueue(){
		//判断队列是否空
		if(isEmpty()){
			//通过抛出异常处理
			throw new RuntimeException("队列空，不能取数据");
		}
		front++;
		return arr[front];
	}
	//显示队列的所有数据
	public void showQueue(){
		//遍历
		if(isEmpty()){
			System.out.println("队列为空，没有数据！");
			return;
		}
		for(int i = 0; i<arr.length;i++){
			System.out.printf("arr[%d]=%d\n",i,arr[i]);
		}
	}
	//显示队列的头数据，注意部署去除数据
	public int headQueue(){
		//判断队列是否为空
		if(isEmpty()){
			throw new RuntimeException("队列空，没有头！");
		}
		return arr[front+1];
	}
}

测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public class ArrayQueueDemo {
	public static void main(String[] args) {
		//创建一个队列
		ArrayQueue arrayQueue = new ArrayQueue(3);
		char key = ' ';//接收用户的输入
		Scanner scanner = new Scanner(System.in);
		boolean loop = true;
		//输出一个菜单
		while(loop){
			System.out.print("s(show):显示队列;");
			System.out.print("e(exit):退出程序;");
			System.out.print("a(add):添加队列;");
			System.out.print("g(get):从队列取出数据;");
			System.out.println("h(head):查看队列头的数据。");
			key = scanner.next().charAt(0);//接收一个字符
			switch (key) {
			case 's':
				arrayQueue.showQueue();
				break;
			case 'e':
				scanner.close();
				loop = false;
				break;
			case 'a':
				try {
					System.out.println("请输入一个数字：");
					int value = scanner.nextInt();
					arrayQueue.addQueue(value);
				} catch (Exception e) {
					System.out.println(e.getMessage());
				}
				break;
			case 'g':
				try {
					int res = arrayQueue.getQueue();
					System.out.printf("取出的数据是%d\n",res);
				} catch (Exception e) {
					System.out.println(e.getMessage());
				}
				break;
			case 'h':
				try {
					int head = arrayQueue.headQueue();
					System.out.printf("队列头为%d\n",head);
				} catch (Exception e) {
					System.out.println(e.getMessage());
				}
				break;
			default:
				break;
			}
		}
		System.out.println("程序退出");
	}
}

结果：
在这里插入图片描述
目前代码存在的一些问题
(1)目前数字使用一次就不能使用，没有达到复用的效果
(2)将这个数字使用算法，改成一个环形的数组

数组模拟环形队列

  • 思路：
    1、front变量的含义做一个调整：front指向队列的第一个元素，也就是说arr[front]就是队列的第一个元素，front的初始值 = 0
    2、rear变量的含义也做一个调整：rear指向队列的最后一个元素的后一个位置，因为希望空出一个空间作为一个约定。rear的初始值 = 0
    3、当队列满时，条件是：( rear + 1 ) % maxSize = front
    4、当队列为空，条件是：rear == front
    5、当这样之后，队列中有效的数据的个数为( rear + maxSize - front ) % maxSize

  • 代码实现
    模拟一个环形队列实例

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    //使用数组模拟环形队列（编写一个CircleQueue类）
    class CircleArray{
    	private int maxSize;//表示数组的最大容量
    	private int front;//front变量的含义做一个调整：front指向队列的第一个元素，也就是说arr[front]就是队列的第一个元素，front的初始值 = 0
    	private int rear;//rear变量的含义也做一个调整：rear指向队列的最后一个元素的后一个位置，因为希望空出一个空间作为一个约定。rear的初始值 = 0
    	private int[] arr;//该数组用于存放队列，模拟的队列
    	//创建队列构造器
    	public CircleArray(int arrMaxSize){
    		maxSize = arrMaxSize;
    		arr = new int[maxSize];
    	}
    	//判断队列是否满
    	public boolean isFull(){
    		return (rear+1)%maxSize==front;
    	}
    	//判断队列是否为空
    	public boolean isEmpty(){
    		return rear == front;
    	}
    	//添加数据到环形队列
    	public void addQueue(int n){
    		//判断队列是否满
    		if(isFull()){
    			throw new RuntimeException("队列满，不能加入数据！");
    		}
    		arr[rear] = n;
    		rear = (rear+1)%maxSize;//将rear后移，这里必须考虑取模
    	}
    	//数据出队列
    	public int getQueue(){
    		//判断队列是否空
    		if(isEmpty()){
    			//通过抛出异常处理
    			throw new RuntimeException("队列空，不能取数据");
    		}
    		//front是指向队列的第一个元素
    		//1、先把front对应的值保存到一个临时的变量
    		//2、将front后移
    		//3、将临时保存的变量返回
    		int value = arr[front];
    		front = (front+1)%maxSize;
    		return value;
    	}
    	//显示队列的所有数据
    	public void showQueue(){
    		//遍历
    		if(isEmpty()){
    			System.out.println("队列为空，没有数据！");
    			return;
    		}
    		//从fron开始遍历，遍历多少个元素
    		for(int i = front; i<front+size();i++){
    			System.out.printf("arr[%d]=%d\n",i%maxSize,arr[i%maxSize]);
    		}
    	}
    	//求出当前队列的有效数据
    	public int size(){
    		return (rear+maxSize-front)%maxSize;
    	}
    	//显示队列的头数据，注意不是去除数据
    	public int headQueue(){
    		//判断队列是否为空
    		if(isEmpty()){
    			throw new RuntimeException("队列空，没有头！");
    		}
    		return arr[front];
    	}
    }

测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
public static void main(String[] args) {
	//测试
	System.out.println("测试环形队列");
	//创建一个队列
	CircleArray circleQueue = new CircleArray(4);//起队列的有效数据最大为3
	char key = ' ';//接收用户的输入
	Scanner scanner = new Scanner(System.in);
	boolean loop = true;
	//输出一个菜单
	while(loop){
		System.out.print("s(show):显示队列;");
		System.out.print("e(exit):退出程序;");
		System.out.print("a(add):添加队列;");
		System.out.print("g(get):从队列取出数据;");
		System.out.println("h(head):查看队列头的数据。");
		key = scanner.next().charAt(0);//接收一个字符
		switch (key) {
		case 's':
			circleQueue.showQueue();
			break;
		case 'e':
			scanner.close();
			loop = false;
			break;
		case 'a':
			try {
				System.out.println("请输入一个数字：");
				int value = scanner.nextInt();
				circleQueue.addQueue(value);
			} catch (Exception e) {
				System.out.println(e.getMessage());
			}
			break;
		case 'g':
			try {
				int res = circleQueue.getQueue();
				System.out.printf("取出的数据是%d\n",res);
			} catch (Exception e) {
				System.out.println(e.getMessage());
			}
			break;
		case 'h':
			try {
				int head = circleQueue.headQueue();
				System.out.printf("队列头为%d\n",head);
			} catch (Exception e) {
				System.out.println(e.getMessage());
			}
			break;
		default:
			break;
		}
	}
	System.out.println("程序退出");
}

结果：
在这里插入图片描述